236. 二叉树的最近公共祖先

link

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

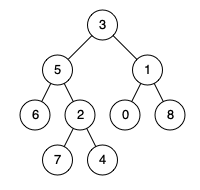
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

思路

自底向上查找即可（回溯），后序遍历天然满足这个条件。接下来就看如何判断一个节点是节点q和节点p的公共祖先。

首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点 p，右子树出现节点 q，或者左子树出现结点 q，右子树出现节点 p，那么该节点就是节点 p 和 q 的最近公共祖先。即情况一：

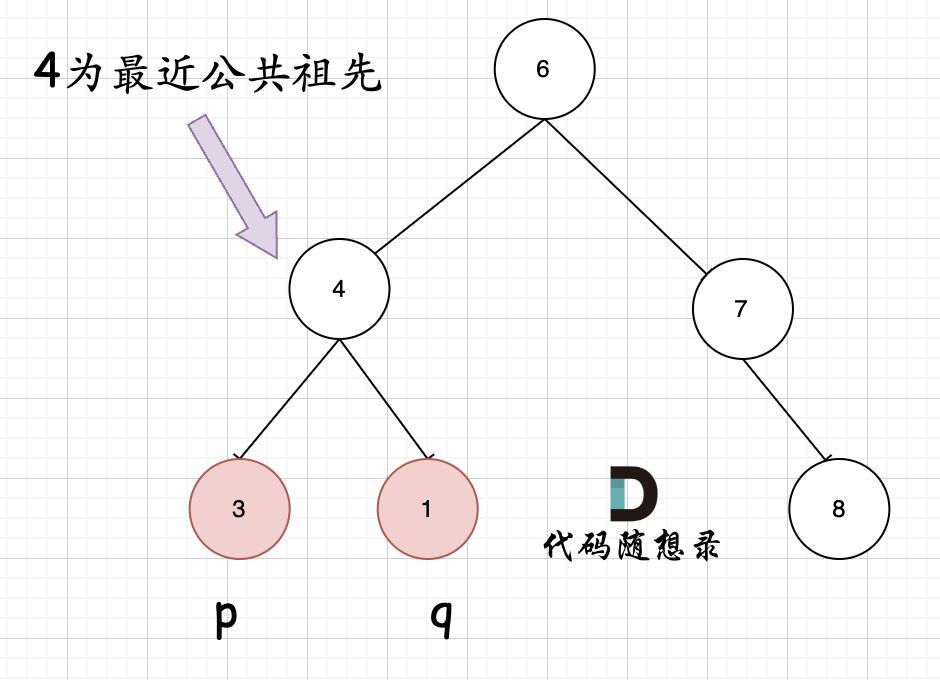
判断逻辑是如果递归遍历遇到 q，就将 q 返回，遇到 p 就将 p 返回，那么如果左右子树的返回值都不为空，说明此时的中节点，一定是 q 和 p 的最近祖先。

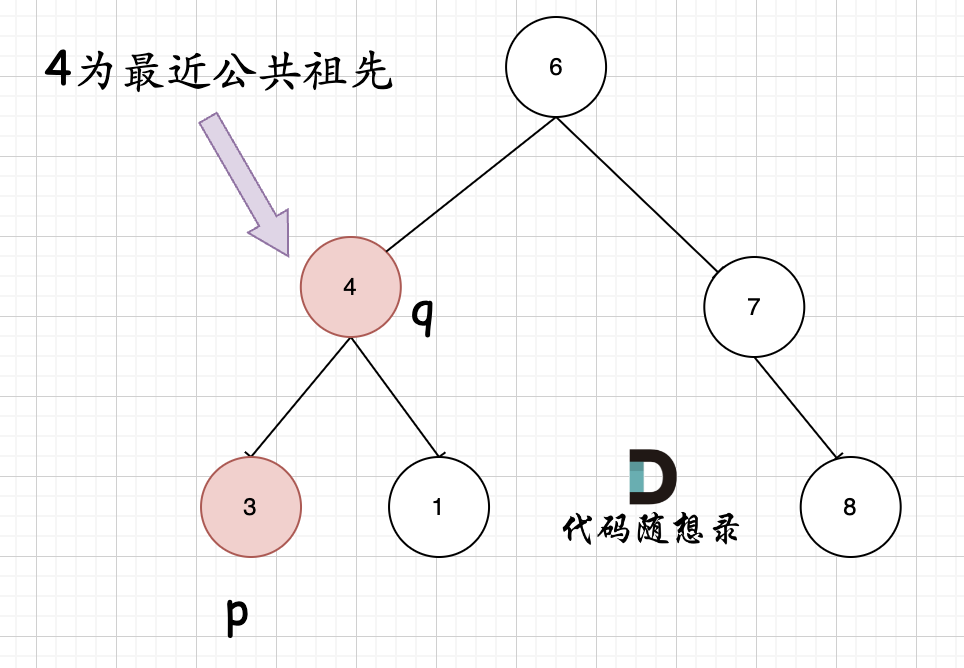
接着是情况二，q 或者 p 为祖先节点：

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        def dfs(node):
            # 找到p或者q，或者为空
            if node == p or node == q or node == None:
                return node

            # 分别在左右子树去找
            lres = dfs(node.left)
            rres = dfs(node.right)

            # 左边右边都找到了，直接返回当前节点
            if lres and rres:
                return node
            # 在左（右）边找到，可能是找到p（q），
            # 也可能是找到了公共节点，回溯去判断。
            if lres:
                return lres
            if rres:
                return rres

            return None

        return dfs(root)

注意，情况 2 在第一个 if 就判断了，例如对于例子中的 6，判断不为 q 或者 p，则访问其子节点，左边直接返回 q，右边返回 None，此时就直接返回 q 为最终结果了。因为在左边查找到了一个节点，右边为空，则说明两个节点一定在一个子树上，所以直接返回找到的 q。

235. 二叉搜索树的最近公共祖先

link

在上一题的基础上添加了限制为二叉搜索树。

思路

搜索二叉树是有序的，所以最近公共子节点一定在区间 [q, p] 或者 [p, q] 中。那么只要从上到下去遍历，遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是p 和 q的公共祖先。那问题来了，一定是最近公共祖先吗？

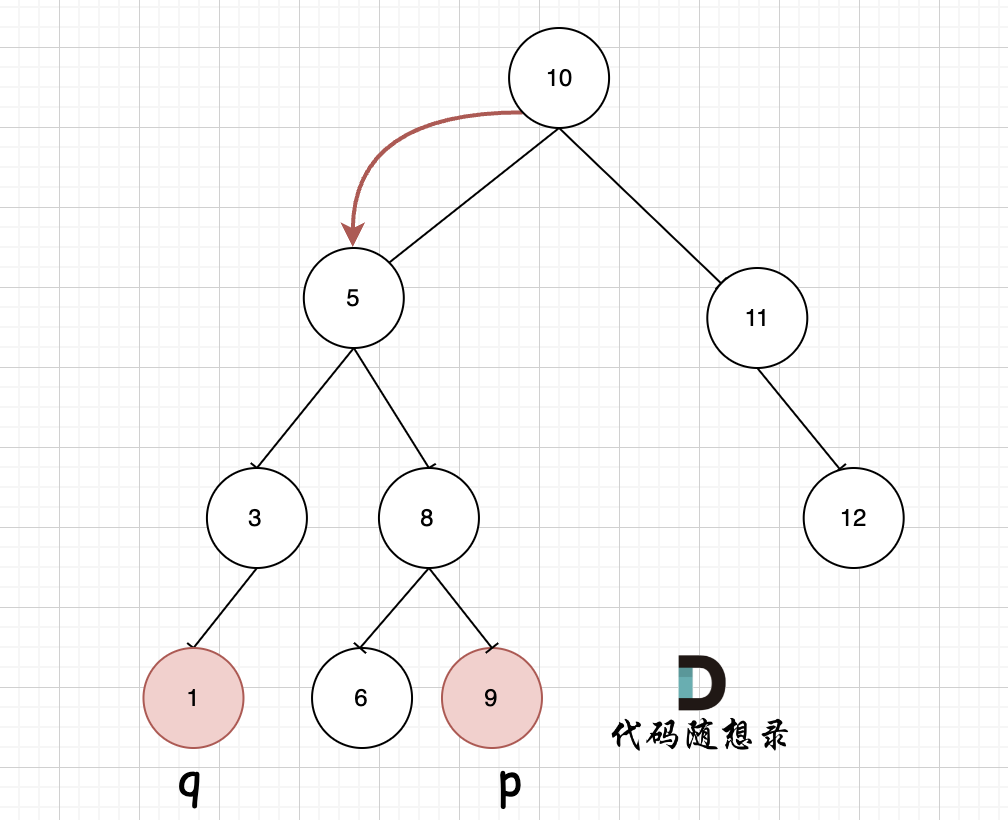
如图所示，首先遍历到 10，q p 都小于 10，则遍历左子树，第一次遇到 5，满足条件，p q 一定一个在左边一个在右边，如何再遍历，则后续节点都不是公共祖先了。

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        stack = []
        if root:
            stack.append(root)
        while stack:
            cur = stack.pop()
            if (min(q.val, p.val) <= cur.val <= max(q.val, p.val)):
                return cur
            if cur.val > max(q.val, p.val):
                stack.append(cur.left) 
            if cur.val < min(q.val, p.val):
                stack.append(cur.right)