226.翻转二叉树

link

翻转一颗二叉树

思路

前序遍历或者后续遍历，在访问当前节点的时候就翻转节点的两个子树。

递归写法

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        def treverse(node):
            if node != None:
                temp = node.right
                node.right = node.left
                node.left = temp

                treverse(node.left)
                treverse(node.right)
        
        treverse(root)

        return root

迭代写法（统一的思路）

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        
        stack = []
        if root != None:
            stack.append(root)
        
        while stack:
            cur = stack.pop()
            if cur != None:
                # 右节点入栈
                if cur.right:
                    stack.append(cur.right)

                # 左节点入栈
                if cur.left:
                    stack.append(cur.left)

                # 中间节点入栈
                stack.append(cur)
                stack.append(None)

            else:
                cur = stack.pop()
                temp = cur.left
                cur.left = cur.right
                cur.right = temp

        return root

106.从中序与后序遍历序列构造二叉树

link

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

思路

明确：

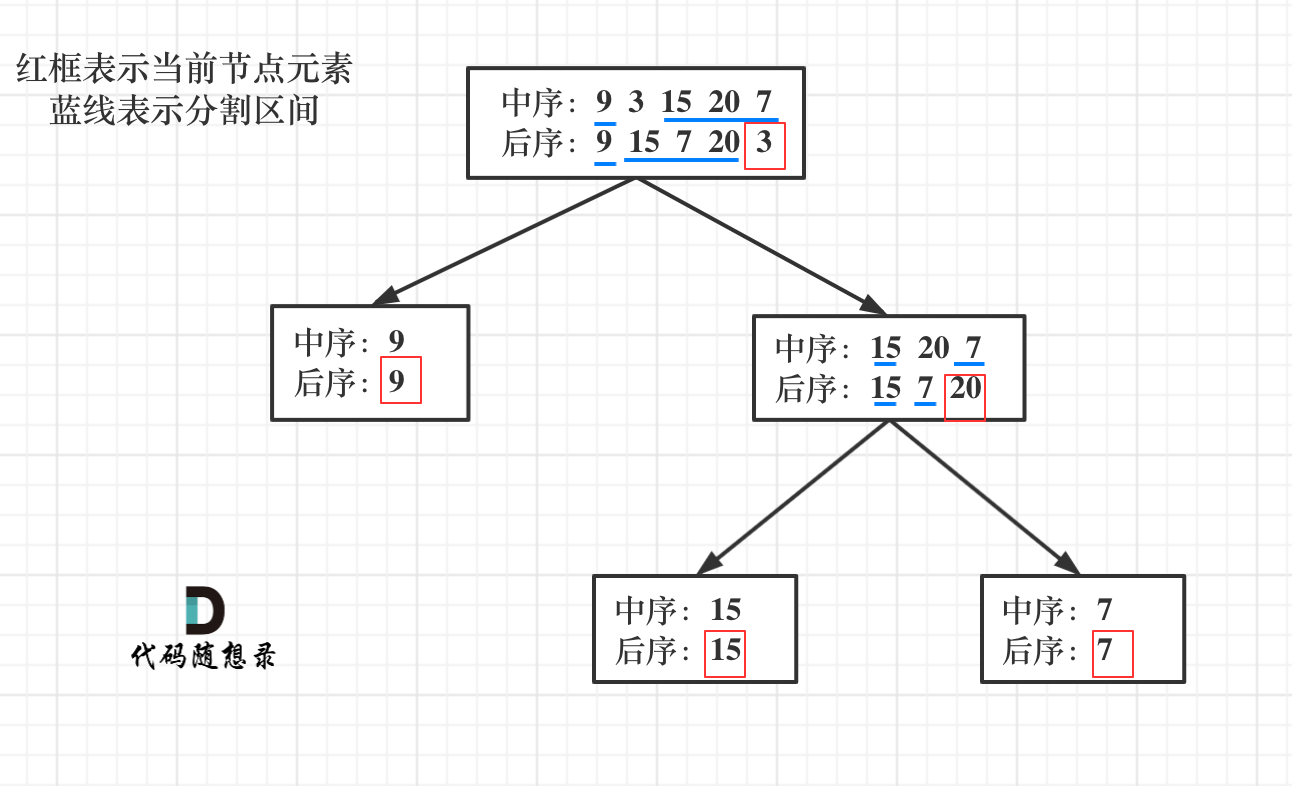
后序遍历的性质：后序遍历的最后一个元素一定是整棵树的根节点。即 postorder = [左子树…, 右子树…, 根]
中序遍历的性质：在中序遍历中，根节点左边的元素是左子树，右边的是右子树。

过程如下：

从后序遍历中取出最后一个元素作为根节点；
在中序遍历中找到这个根节点的位置；
递归构建左右子树：
- 中序左边部分 → 左子树
- 中序右边部分 → 右子树
- 后序中要对应分成左子树和右子树的区间

注意在递归中，要优先处理右子树，因为右子树更靠近根节点，需要先 pop（但是为什么不需要手动切片？这里的 posto 不是局部变量吗？）

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        
        def make(ino, posto):
            if not ino or not posto:
                return None
            val = posto.pop()
            index = ino.index(val)
            root = TreeNode(val)

            subinleft = ino[0:index]
            subinright = ino[index+1:]

            root.right = make(subinright, posto)
            root.left = make(subinleft, posto)
            return root
        return make(inorder, postorder)

105. 从前序与中序遍历序列构造二叉树

link

类似于上一题，只不过由于前序遍历是根节点在索引 0，无法动态更新数组，所以需要进行手动切片，此时就不需要在乎先处理哪个子树了，因为已经显示地指定。上一题需要先处理右子树，是因为需要在递归的过程中多次修改 posto 数组。

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        def make(ino, posto):
            if not ino or not posto:
                return None
            val = posto[0]
            index = ino.index(val)
            root = TreeNode(val)
            subinleft = ino[0:index]
            subinright = ino[index+1:]
            root.left = make(subinleft, posto[1:len(subinleft)+1])
            root.right = make(subinright, posto[len(subinleft)+1:])
            return root

        return make(inorder, preorder)

小总结

前序和中序可以唯一确定一棵二叉树。
后序和中序可以唯一确定一棵二叉树。
但是前序和后序不能唯一确定一棵二叉树！

因为无法确定根节点，就无法进行分割

654.最大二叉树

link

给定一个不重复的整数数组 nums 。最大二叉树可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的子数组前缀上构建左子树。
递归地在最大值右边的子数组后缀上构建右子树。

思路

类似于构造二叉树，思路在题目中已经给出

class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        
        def make(num_list):
            if not num_list:
                return None
            max_num = max(num_list)
            index = num_list.index(max_num)

            root = TreeNode(max_num)

            root.left = make(num_list[:index])
            root.right = make(num_list[index+1:])

            return root
        
        return make(nums)

617.合并二叉树

link

同时遍历两颗树即可。注意递归的主逻辑判断，当一个节点为空时，直接返回另一个节点，不用考虑另一个节点是否为空。只有两个节点都不为空的时候才需要单独判断。

class Solution:
    def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
        
        def make(node1, node2):
            if node1 == None:
                return node2
            if node2 == None:
                return node1
            
            cur = TreeNode(node1.val + node2.val)
            cur.left = make(node1.left, node2.left)
            cur.right = make(node1.right, node2.right)

            return cur
        
        return make(root1, root2)