53. 最大子序和

link

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。子数组是数组中的一个连续部分。

思路

局部最优：当前累加和是正的，就继续累加；否则重新开始。如果当前累加的子数组和 cur_sum 小于 0，那它对后面的结果毫无贡献，直接舍弃，从下一个元素重新开始。

全局最优：过程中不断维护最大值。

同时记得每添加一次都需要更新当前的最大值

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        cur = 0
        maxi = float('-inf')
        for i in nums:
            cur += i
            maxi = max(cur, maxi)
            if cur < 0:
                cur = 0
        return maxi

134. 加油站

link

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则保证它是唯一的。

暴力

两层循环，分别遍历起点和跑一圈，如果能重新到达起点，则说明当前起点满足条件。

贪心

如果总油量小于总消耗量，则说明无论如何都不能满足条件。然后从 0 开始遍历，记录从头开始的油箱剩余量（rest += gas[i] - cost[i]）。如果某个步骤 i 判断 rest 小于 0，则说明从当前起点 start 开始，最远只能跑到 i。此时把起点设置为 i+1，重新开始遍历。（只用遍历到末尾即可，因为上一步是从 0 开始，（等价于末尾），最远到 i，而第二步是从 i+1 开始遍历到末尾，（等价是 0），相当于跑了一圈）

如果 tank < 0，说明从起点走到当前 i 失败了：当前这一段不能作为起点。
所以我们跳过它，从 i+1 开始重新尝试，把 tank 重置为 0。

虽然某些起点不行，但我们只要跳过这些亏损段（tank<0 的段），并且：

总的供油是 ≥ 总耗油的
那么在某个位置之后，盈余就能把之前的亏空补回来
也就是说，之前亏了多少，后面就能“补回来”，最终一定可以绕一圈。

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        if sum(gas) < sum(cost):
            return -1
        cur = 0
        start = 0

        for i in range(len(gas)):
            cur += gas[i] - cost[i]
            if cur < 0:
                start = i + 1
                cur = 0

        return start

968. 监控二叉树

link

给定一个二叉树，我们在树的节点上安装摄像头。节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。计算监控树的所有节点所需的最小摄像头数量。

思路

核心：摄像头不能放在叶子节点上。摄像头可以覆盖上中下三层，如果把摄像头放在叶子节点上，就浪费的一层的覆盖。所以把摄像头放在叶子节点的父节点位置，才能充分利用摄像头的覆盖面积。

局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少

需要从下向上遍历，只有使用后序遍历。在遍历的过程中需要进行状态转移。定义三种状态：
有如下三种：

该节点无覆盖
本节点有摄像头
本节点有覆盖

分别有三个数字来表示：

0：该节点无覆盖
1：本节点有摄像头
2：本节点有覆盖

递归三部曲：

参数和返回值：需要返回当前节点的状态
终止条件：遇到空就返回，注意空节点应该定义为有覆盖（2）（否则该叶子节点就需要放摄像头了）
核心逻辑：
- 左右都有覆盖（两个 2），当前节点就为无覆盖（0）
- 至少一个孩子没有覆盖（至少一个 0），那就要放摄像头（1）
- 至少一个孩子放了摄像头（至少一个 1），当前节点就有覆盖（2）

注意上述顺序不能打乱，下面的情况应该是 1，而不是 2。

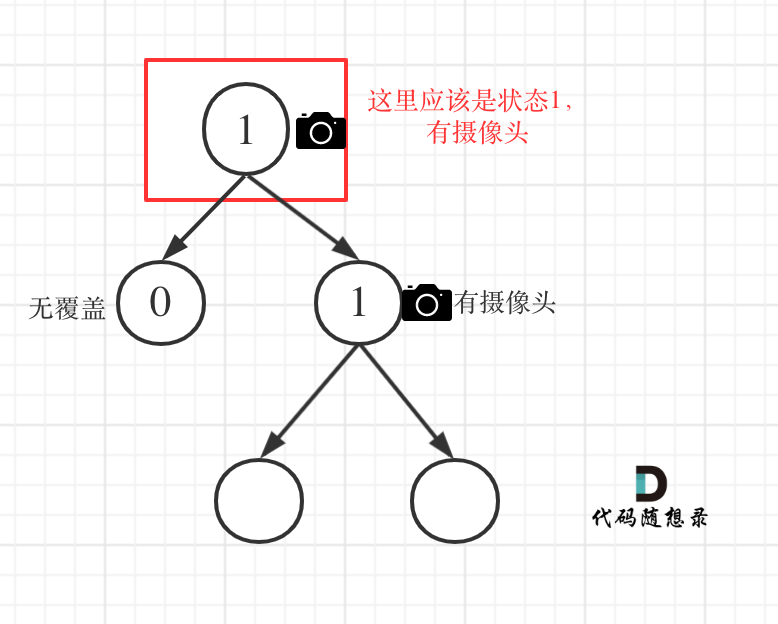
此外，如果根节点没有覆盖，也需要放摄像头。

class Solution:
    def minCameraCover(self, root: Optional[TreeNode]) -> int:
        res = [0]
        def treverse(node):
            if node == None:
                return 2
            
            left = treverse(node.left)
            right = treverse(node.right)

            if left == 2 and right == 2:
                return 0

            if left == 0 or right == 0:
                res[0] += 1
                return 1
            
            if left == 1 or right == 1:
                return 2
        
        if treverse(root) == 0:
            res[0] += 1
        return res[0]