【代码随想录】贪心算法5-区间问题

55. 跳跃游戏

link

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个位置。

示例：

输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

思路

贪心思想为，每一步都跳最远，然后考虑每个元素作为起点时，是否能跳到末尾，代码如下：

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        n = len(nums)
        for i in range(n):
            pos = i
            while pos < n:
                if nums[pos] == 0 and pos != n - 1:
                    break
                if pos + nums[pos] >= n - 1:
                    return True
                pos += nums[pos]  # 贪心跳到最远
        return False

但是无法处理 [3,2,1,0,4] 情况，因为外层的 for 循环会跳过 0 这个点，直接到最后。

正确的思路为，遍历每一个点，记录能跳到的最远距离 cover。而只在 cover 这个范围中进行遍历（cover 动态更新）。如果某一步的 cover 大于终点，则返回 True。如果循环遍历完了，说明 cover 仍然小于终点，则返回 False。

• 局部：每次都跳最远，记录能跳的最长距离
• 全局：最后得到整体最大覆盖范围，看是否能到终点。

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        n = len(nums)
        i = 0
        cover = 0

        while i <= cover:
            if cover >= n - 1:
                return True
            cover = max(nums[i] + i, cover)
            i += 1

        return False

本质上，第二段代码已经覆盖了第一段代码的流程。因为我们每次是在 cover 里面遍历，在 cover 中无论如何都能到达，所以就不需要遍历起点。

45.跳跃游戏 II

link

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

思路

贪心的思路，局部最优：当前可移动距离尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最少步数。

解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最少步数。需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。

注意这一题明确了一定可以跳到：

• 首先在当前这一步的距离 cur 中遍历，找到下一步的最大范围 nex（cur 范围内只需要一个步骤就能跳到）
• 如果遍历到了 cur 的末尾，说明当前步骤跳不到，则 res 加 1（表示跳到 nex 范围中），并将 nex 赋值给 cur
• 如果 cur 已经超过终点，则直接返回。（贪心的点在于每次都是跳最远的）（注意要在赋值之后才判断）

class Solution:
    def jump(self, nums: List[int]) -> int:
        cur = 0
        nex = 0
        res = 0
        if len(nums) == 1:
            return 0
        for i in range(len(nums)):
            nex = max(nums[i] + i, nex)
            if i == cur:
                res += 1
                cur = nex

                if cur >= len(nums) - 1:
                    return res

452. 用最少数量的箭引爆气球

link

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。

示例：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
在x = 6处射出箭，击破气球[2,8]和[1,6]。
在x = 11处发射箭，击破气球[10,16]和[7,12]。

思路

需要将气球进行排序，需要维护一个当前箭能覆盖到的最右位置（当前重叠区间的右边界）。

如果当前气球的开始点大于最右边界，说明当前箭射不到这个气球；如果能满足，则需要更改最大右边界，为了解决 [1, 6] 和 [2, 4] 这种情况。类似于上面的 55. 跳跃游戏，虽然第一支箭最元能从 6 射出（贪心，射最远的点），第二个气球的起点在当前最大射程之内，即一定满足，需要更新最大射程为 4.（即最远能从 6 射，但是不一定从 6 射）

class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        points.sort(key=lambda x: (x[0], x[1]))
        res = 1
        rightboder = points[0][1]
        for i in points:
            if i[0] > rightboder:
                res += 1
                rightboder = i[1]
            else:
                rightboder = min(i[1], rightboder)

        return res

435. 无重叠区间

link

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。注意 只在一点上接触的区间是 不重叠的。例如 [1, 2] 和 [2, 3] 是不重叠的。

思路

将有重叠的区间视为一个整体，本质上是判断所有的区间可以分为几个“整体”。也就是说，每个整体中最多只能包含一个区间，多余的区间就要删除掉。本质上就类似与上一题 452. 用最少数量的箭引爆气球。箭的数量就代表有几个整体，总的数量减去箭的数量就代表要删除的数量。

所以就是要维护一个最右边界：

• 如果当前区间的左边界比当前最右边界小，说明重叠，然后更新最右边界。注意，为了将来有更多不重叠区间被保留，需要保留右边界更小的区间
• 如果当前区间的左边界比当前最右边界大，说明没有重叠，“整体”的数量加一

贪心的点在于：优先保留结束早的区间，以便为后续留出更多空间

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        intervals.sort(key=lambda x: (x[0], x[1]))
        count = 1
        rightboder = intervals[0][1]

        for i in intervals:
            if i[0] >= rightboder:
                count += 1
                rightboder = i[1]
            else:
                rightboder = min(rightboder, i[1])
        
        return len(intervals) - count

763.划分字母区间

link

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。例如，字符串 “ababcc” 能够被分为 [“abab”, “cc”]，但类似 [“aba”, “bcc”] 或 [“ab”, “ab”, “cc”] 的划分是非法的。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。返回一个表示每个字符串片段的长度的列表。

思路 1

题目要求同一字母最多出现在一个片段中，在遍历的过程中相当于是要找每一个字母的边界，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了。

两个步骤：

• 统计每一个字符最后出现的位置
• 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

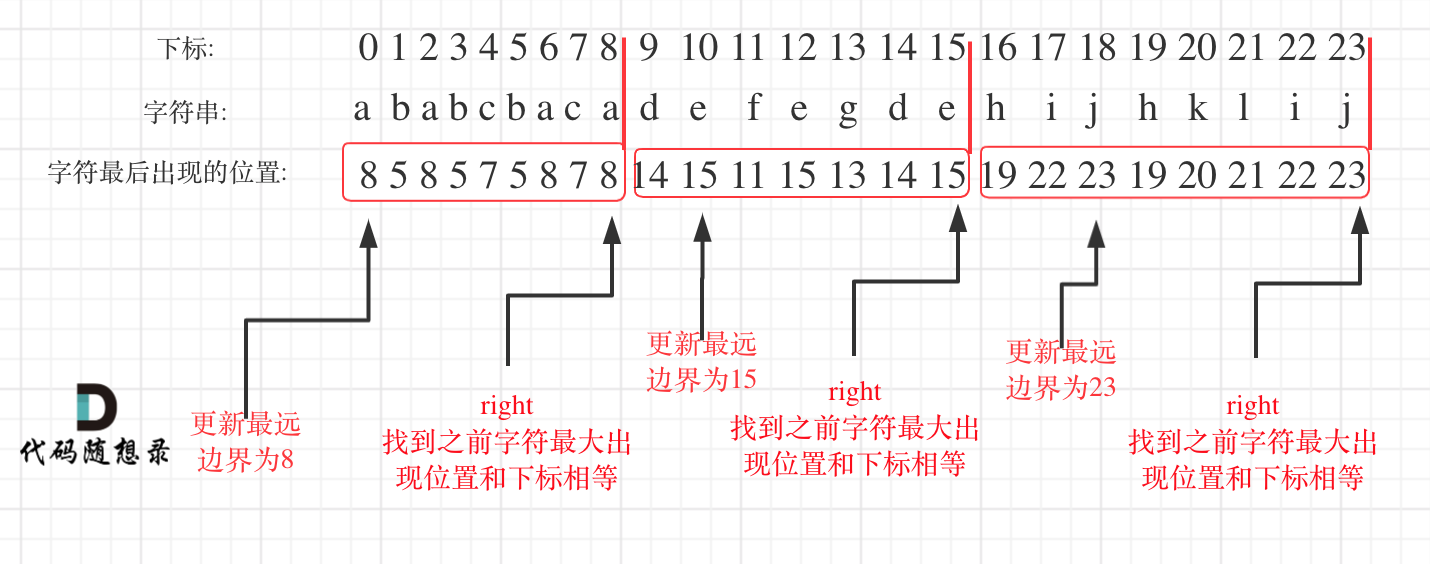
注意当前的区间必须要覆盖到当前所有字符的最后一次出现位置，所以 right = max(right, m[ch])。

class Solution:
    def partitionLabels(self, s: str) -> List[int]:
        m = {}
        for i, ch in enumerate(s):
            m[ch] = i
        res = []
        right = 0
        left = 0
        for i, ch in enumerate(s):
            right = max(right, m[ch])
            if right == i:
                res.append(right - left + 1)
                left = i + 1
        return res

思路 2

类似于前两题 452.用最少数量的箭引爆气球 和 435.无重叠区间，统计字符串中所有字符的起始和结束位置，记录这些区间（实际上也就是 435.无重叠区间 题目里的输入），将区间按左边界从小到大排序，找到边界将区间划分成组，互不重叠。找到的边界就是答案。

本质上是要把有重叠的区间（说明对应的字符串要放在一起）合并。

class Solution:
    def countLabels(self, s):
        # 初始化一个长度为26的区间列表，初始值为负无穷
        hash = [[float('-inf'), float('-inf')] for _ in range(26)]
        hash_filter = []
        for i in range(len(s)):
            if hash[ord(s[i]) - ord('a')][0] == float('-inf'):
                hash[ord(s[i]) - ord('a')][0] = i
            hash[ord(s[i]) - ord('a')][1] = i
        for i in range(len(hash)):
            if hash[i][0] != float('-inf'):
                hash_filter.append(hash[i])
        return hash_filter

    def partitionLabels(self, s):
        res = []
        hash = self.countLabels(s)
        hash.sort(key=lambda x: x[0])  # 按左边界从小到大排序
        rightBoard = hash[0][1]  # 记录最大右边界
        leftBoard = 0
        for i in range(1, len(hash)):
            if hash[i][0] > rightBoard:  # 出现分割点
                res.append(rightBoard - leftBoard + 1)
                leftBoard = hash[i][0]
            rightBoard = max(rightBoard, hash[i][1])
        res.append(rightBoard - leftBoard + 1)  # 最右端
        return res

56. 合并区间

link

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6]

思路

类似于前几题，只不过判断出重叠后，需要合并区间。同样先对区间进行排序。

• 注意这里先将第一个区间放到结果集合 res 中，然后每次遍历时都取当前结果 res 的最后一个区间来进行比较，如果 last[1] > i[0]，说明当前有重叠，把最后的区间取出来，合并之后再放进去。
• 注意合并区间时，其实只需要更改结束的点，因为最开始就进行了排序，前一个区间的起始点一定是最小的。

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        intervals.sort(key=lambda x: x[0])
        res = [intervals[0]]
        start = 0
        end = 0
        for i in intervals:
            last = res[-1]
            if last[1] >= i[0]:
                res.pop()
                # 其实只需要改区间的终点
                res.append([min(last[0], i[0]), max(last[1], i[1])])
            else:
                res.append(i)

        return res