59. 螺旋矩阵 II

题目链接 link

给你一个正整数 n ，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例：

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

思路

核心：左闭右开进行填充，每个圈按照以下顺序来画：

填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上

循环变量为要画的圈的数量（偏移量，因为是左闭右开区间，每一行（列）的最后一位不填）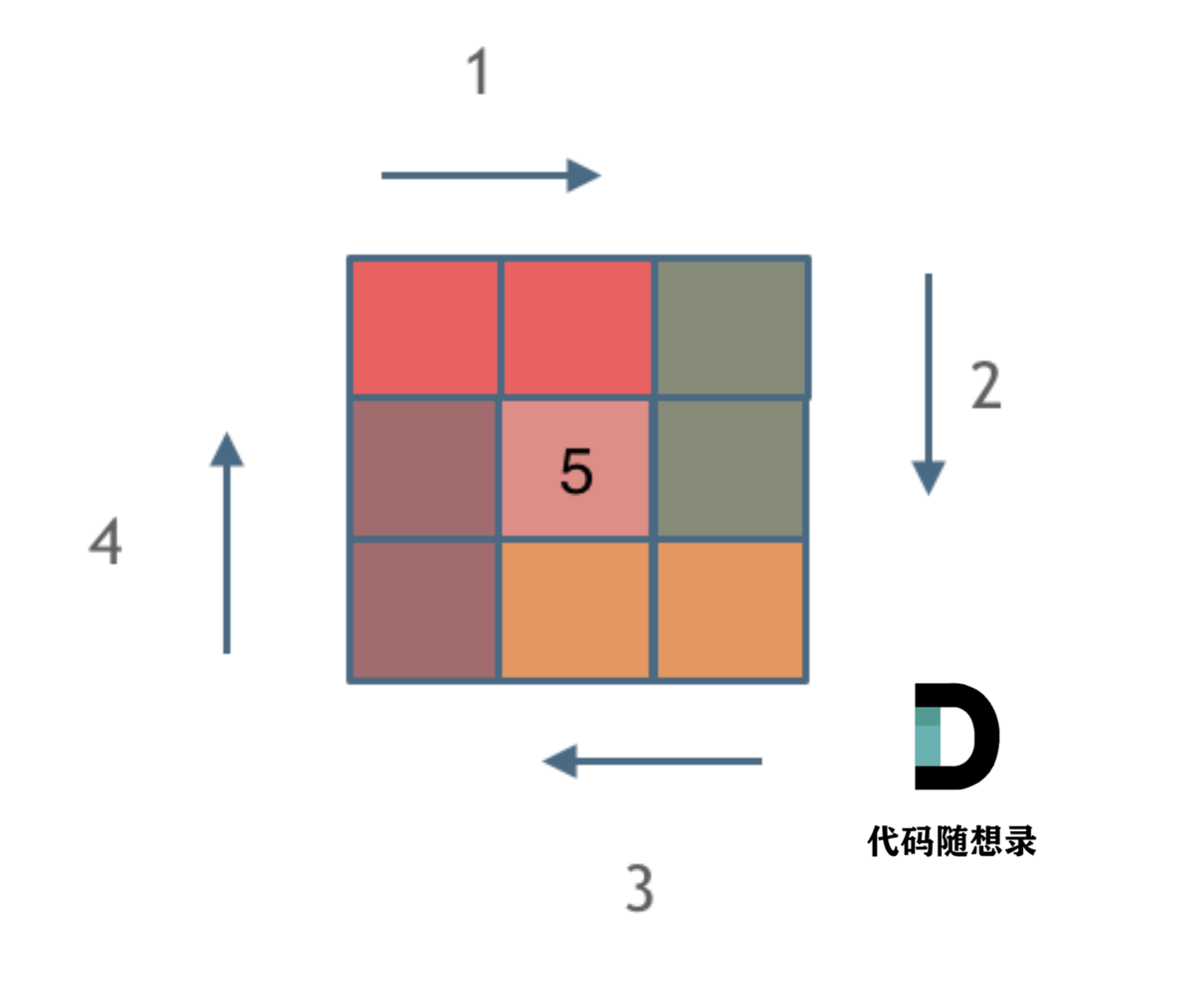

定义：

起点：每一圈的左上角的点

终点：n 减去偏移量

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        res = [[0 for _ in range(n)] for _ in range(n)]
        loop = n // 2
        
        startx, starty = 0, 0
        count = 1
        for offset in range(1, loop + 1):
            for i in range(starty, n - offset):
                res[startx][i] = count
                count += 1

            for i in range(startx, n - offset):
                res[i][n - offset] = count
                count += 1
            
            for i in range(n - offset, starty, -1):
                res[n - offset][i] = count
                count += 1
            
            for i in range(n - offset, startx, -1):
                res[i][starty] = count
                count += 1
            
            startx += 1
            starty += 1

        if n % 2 != 0:
            res[n // 2][n // 2] = count

        return res

54. 螺旋矩阵

题目链接 link

给你一个 m 行 n 列的矩阵 matrix ，请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

思路

上一个题目的扩展，即形状不一定为正方形，有以下几个方面的考虑：

循环的次数（几个 loop）决定于 matrix 的短边
计算偏移量时要注意是长边减去偏移量还是短边
中间部分的处理：
- 如果是正方形，则直接边长 // 2 进行读取
- 如果是长方形，则需要注意：
  - 判断中间部分是哪条边
  - 默认的情况是左闭右开，本来需要将 offset - 1，但是中间部分需要左闭右闭，则 offset 不用 - 1

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        x = len(matrix)
        y = len(matrix[0])
        loop = min(x, y) // 2

        startx = 0
        starty = 0
        res = []
        offset = 0
        for offset in range(1, loop + 1):
            for i in range(starty, y - offset):
                res.append(matrix[startx][i])
            
            for i in range(startx, x - offset):
                res.append(matrix[i][y - offset])
            
            for i in range(y - offset, starty, -1):
                res.append(matrix[x - offset][i])
            
            for i in range(x - offset, startx, -1):
                res.append(matrix[i][starty])

            startx += 1
            starty += 1
        
        if x == y and x % 2 != 0:
            res.append(matrix[x // 2][y // 2])

        elif x > y and y % 2 != 0:
            for i in range(startx, x - offset):
                res.append(matrix[i][y // 2])
        elif x < y and x % 2 != 0:
            for i in range(starty, y - offset):
                res.append(matrix[x // 2][i])
        
        return res