209.长度最小的子数组
题目链接 link
找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
示例 2:
输入:target = 4, nums = [1,4,4]
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
解法1:暴力循环 两个 for 循环即可解决,分别遍历子数组的开头以及子数组内部。使用 python 可能会超出时间限制。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution: def minSubArrayLen(self, target: int, nums: List[int]) -> int: min_len = 0 for i in range(len(nums)): array_sum = 0 for j in range(i, len(nums)): array_sum += nums[j] if array_sum >= target: cur_len = j - i + 1 if min_len == 0 or min_len > cur_len: min_len = cur_len break return min_len
解法2:前缀和+二分查找 方法一中,确定了数组的开始位置,查找结束位置的时间复杂度为 O(n),如果使用二分查找,可以优化到 O(logn)。为了使用二分查找,需要额外创建一个数组 sums 用于存储数组 nums 的前缀和,其中 sums[i] 表示从 nums[0] 到 nums[i−1] 的元素和。得到前缀和之后,对于每个开始下标 i,可通过二分查找得到大于或等于 i 的最小下标 bound,使得 sums[bound]−sums[i−1]≥target,并更新子数组的最小长度(此时子数组的长度是 bound−(i−1))。
相当于是查找特定元素的插入位置,这个值就是题目中给定的 target,但是要注意,当窗口的起始位置不为 0 时,target 需要加上当前窗口的起始前缀和,因为我们的窗口要满足条件 sums[end] - sums[start] >= s,即 sums[end] >= s + sums[start],要找到满足这个条件的 end,所以二分查找的 target1 定义为 target = s + sums[start]。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution: def minSubArrayLen(self, s: int, nums: List[int]) -> int: if not nums: return 0 n = len(nums) ans = n + 1 sums = [0] for i in range(n): sums.append(sums[-1] + nums[i]) for i in range(1, n + 1): target = s + sums[i - 1] bound = bisect.bisect_left(sums, target) if bound != len(sums): ans = min(ans, bound - (i - 1)) return 0 if ans == n + 1 else ans
解法3:滑动窗口 在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环完成了一个不断搜索区间的过程。
只用一个for循环,那么这个循环的索引,一定是表示滑动窗口的终止位置。对于窗口的起始位置,则基于窗口的和来判断是否需要移动。使用一个 while 循环来表示,如果子数组的和大于 target,则减去窗口起始位置的值,并使窗口起始位置 +1。
此外,不要以为for里放一个while就以为是O(n^2), 主要是看每一个元素被操作的次数 ,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution: def minSubArrayLen(self, target: int, nums: List[int]) -> int: min_len = 0 start = 0 array_sum = 0 for end in range(len(nums)): array_sum += nums[end] while array_sum >= target: cur_len = end - start + 1 if min_len == 0 or min_len > cur_len: min_len = cur_len array_sum -= nums[start] start += 1 return min_len
904. 水果成篮
题目链接 link
你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果种类 。
你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必须按照要求采摘水果:
你只有 两个 篮子,并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
示例 1:
输入:fruits = [1,2,1]
示例 2:
输入:fruits = [0,1,2,2]
示例 3:
输入:fruits = [1,2,3,2,2]
示例 4:
输入:fruits = [3,3,3,1,2,1,1,2,3,3,4]
思路 相当于是只包含两个数字的最长子数组,使用了一个 Counter 类,Counter 是一个计数器字典 ,可以自动统计元素出现的次数。pop 方法用于删除指定的 key,并可以返回其 value。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution: def totalFruit(self, fruits: List[int]) -> int: max_len = 0 start = 0 cnt = Counter() for end in range(0, len(fruits)): cnt[fruits[end]] += 1 while len(cnt) > 2: cnt[fruits[start]] -= 1 if cnt[fruits[start]] == 0: cnt.pop(fruits[start]) start += 1 max_len = max(max_len, end - start + 1) return max_len
Counter 类等价于
1 2 cnt = {} cnt[x] = cnt.get(x, 0)
get 方法查找指定 key 对应的 value,找不到时返回默认值,使用原始 dict 的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution: def totalFruit(self, fruits: List[int]) -> int: max_len = 0 start = 0 cnt = dict() for end in range(0, len(fruits)): cnt[fruits[end]] = cnt.get(fruits[end], 0) + 1 while len(cnt) > 2: cnt[fruits[start]] -= 1 if cnt[fruits[start]] == 0: cnt.pop(fruits[start]) start += 1 max_len = max(max_len, end - start + 1) return max_len
76. 最小覆盖子串(Hard)
题目链接 link
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
示例 1:
输入:s = “ADOBECODEBANC”, t = “ABC”
示例 2:
输入:s = “a”, t = “a”
示例 3:
输入: s = “a”, t = “aa”
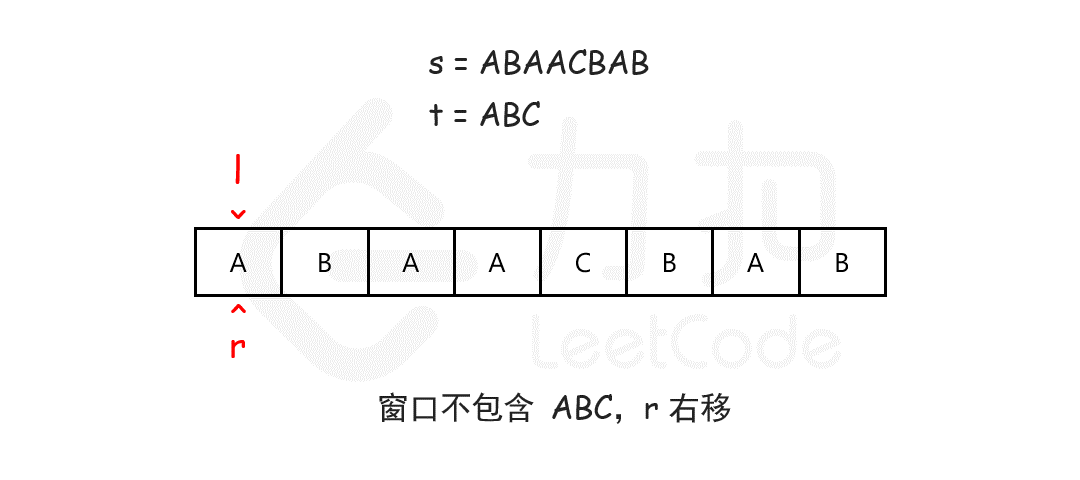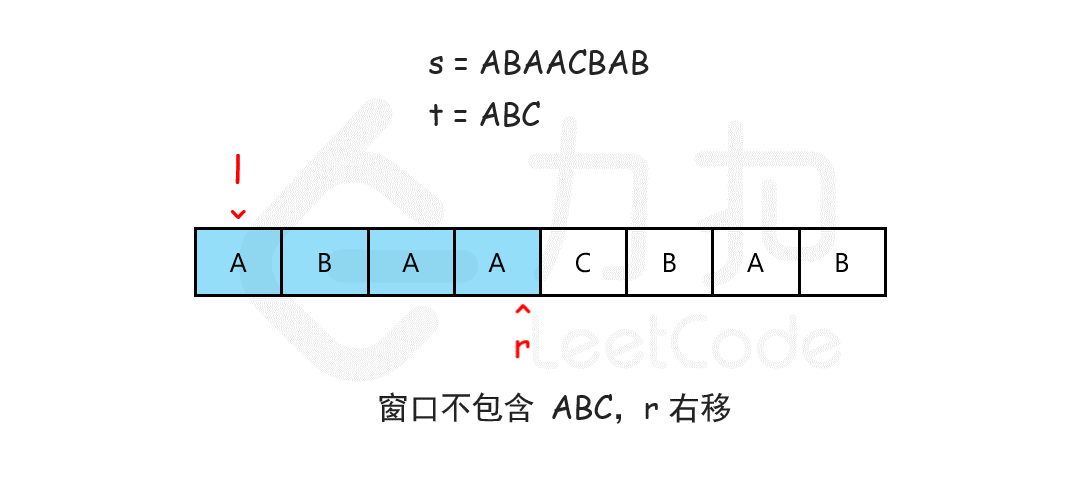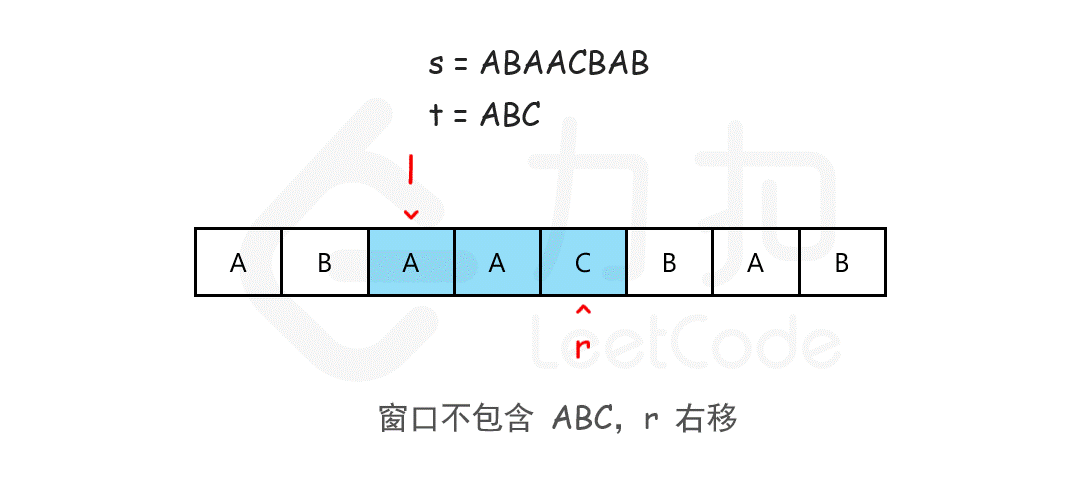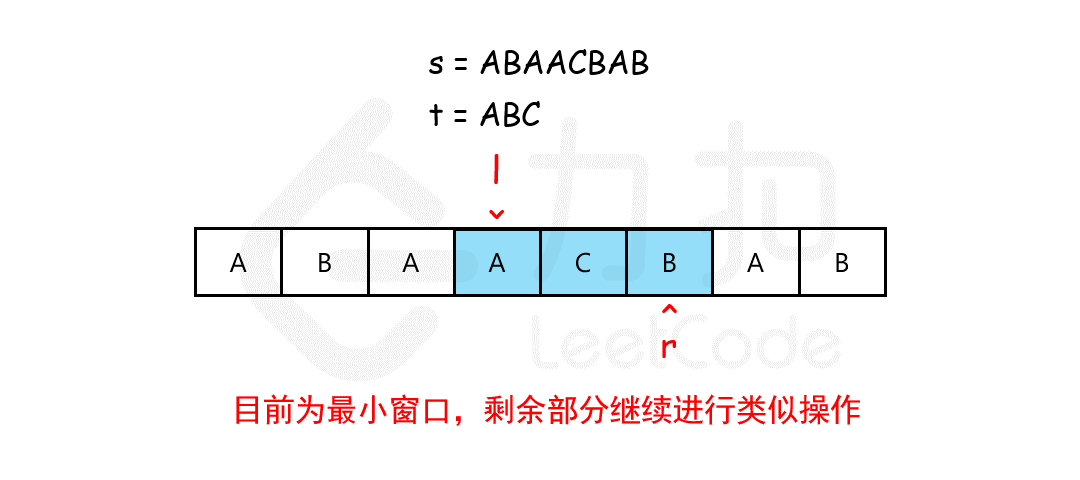
滑动窗口
核心为如何判断当前 s 的窗口是否覆盖了 t。可以使用一个哈希表来记录,同时,t 中可能有重复的字符,所以需要记录字符的个数(两个计数器,需要的字符个数,和当前窗口已经有的个数)。此外,Counter 可以直接使用大于和小于运算符来进行判断是否覆盖。所以可以写出以下代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution: def minWindow(self, s: str, t: str) -> str: min_str = "" s_list = list(s) t_list = list(t) start = 0 t_cnt = Counter() s_cnt = Counter() for i in t_list: t_cnt[i] += 1 for end in range(len(s_list)): s_cnt[s_list[end]] += 1 while s_cnt >= t_cnt: if min_str == "" or len(min_str) > end - start + 1: min_str = "".join(s_list[start: end + 1]) s_cnt[s_list[start]] -= 1 start += 1 return min_str
但是,上述代码会提示超时,原因是每次更新最小子字符串时,都会进行切片操作, 也是新建字符串对象(O(end - start),所以可以使用两个变量 ans_start 和 ans_end 来记录对应的下标,只在最后对字符串进行操作。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution: def minWindow(self, s: str, t: str) -> str: s_list = list(s) t_list = list(t) start = 0 t_cnt = Counter() s_cnt = Counter() ans_start = 0 ans_end = len(s) for i in t_list: t_cnt[i] += 1 for end in range(len(s_list)): s_cnt[s_list[end]] += 1 while s_cnt >= t_cnt: if ans_end == len(s) or ans_end - ans_start > end - start: ans_end = end ans_start = start s_cnt[s_list[start]] -= 1 start += 1 if ans_end == len(s): return "" else: return "".join(s_list[ans_start: ans_end + 1])
Counter 本质上是一个 dict,如果使用 dict,需要定义一个判断函数,注意,这里是遍历了 t 对应的 dict,即需要的字符数量,时间复杂度为 O(|len(t)|),dict 为哈希表,读写的时间复杂度为 O(1)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution: def minWindow(self, s: str, t: str) -> str: s_list = list(s) t_list = list(t) start = 0 t_cnt = dict() s_cnt = dict() ans_start = 0 ans_end = len(s) for i in t_list: t_cnt[i] = t_cnt.get(i, 0) + 1 for end in range(len(s_list)): s_cnt[s_list[end]] = s_cnt.get(s_list[end], 0) + 1 while self.check(s_cnt, t_cnt): if ans_end == len(s) or ans_end - ans_start > end - start: ans_end = end ans_start = start s_cnt[s_list[start]] -= 1 start += 1 if ans_end == len(s): return "" else: return "".join(s_list[ans_start: ans_end + 1]) def check(self, s_cnt1, t_cnt1): for key, value in t_cnt1.items(): if value > s_cnt1.get(key, 0): return False return True