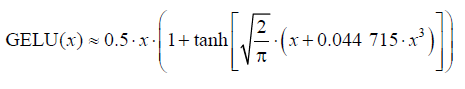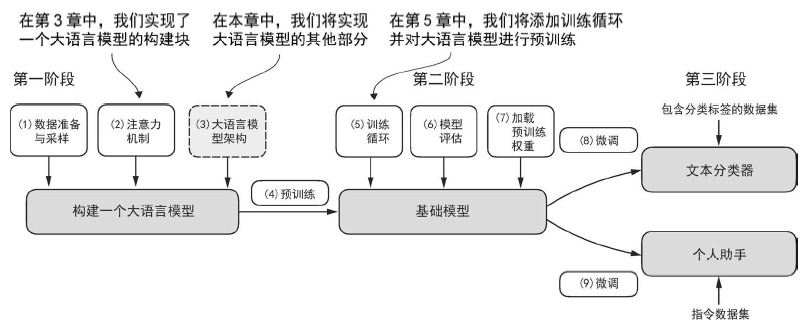
构建一个大语言模型架构

大语言模型包含以下内容：

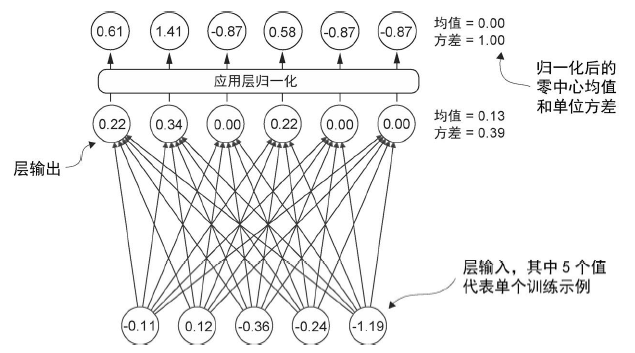
使用层归一化进行归一化激活

层归一化的主要思想是调整神经网络层的激活（输出），使其均值为 0 且方差（单位方差）为 1。这种调整有助于加速权重的有效收敛，并确保训练过程的一致性和可靠性。

注意，上图中的输入表示一个输入，层归一化是在特征维度进行。代码实现如下：

class LayerNorm(nn.Module):
    #layer归一化的函数,可以避免信息泄露也可以稳定
    def __init__(self, emb_dim):
        super().__init__()
        self.eps = 1e-5 #避免0的产生导致崩溃
        self.scale = nn.Parameter(torch.ones(emb_dim)) #动态的缩放参数
        self.shift = nn.Parameter(torch.zeros(emb_dim)) #动态的偏移参数

    def forward(self, x):
        mean = x.mean(dim=-1, keepdim=True)#算平均值
        var = x.var(dim=-1, keepdim=True, unbiased=False)#算方差
        norm_x = (x - mean) / torch.sqrt(var + self.eps)#归一化
        return self.scale * norm_x + self.shift #通过两个可学习的参数调整归一化后的值范围和位置

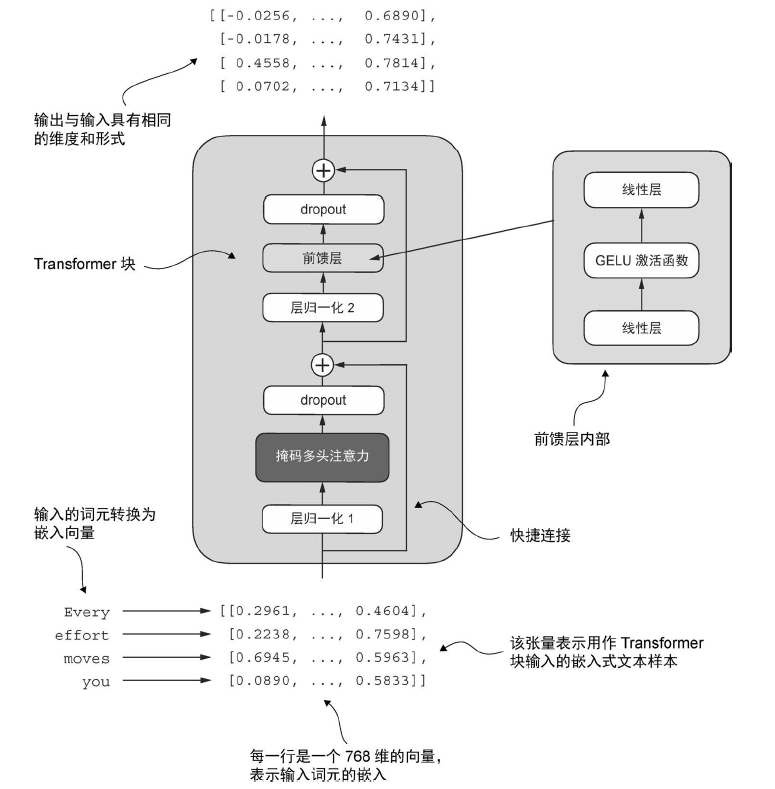
实现具有 GELU 激活函数的前馈神经网络

GELU 和 SwiGLU 是更为复杂且平滑的激活函数，分别结合了高斯分布和 sigmoid 门控线性单元。与较为简单的 ReLU 激活函数相比，它们能够提升深度学习模型的性能。一种近似实现如下：

class GELU(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, x):
        return 0.5 * x * (1 + torch.tanh(
            #这一步把它变得平滑了很多
            torch.sqrt(torch.tensor(2.0 / torch.pi)) * 
            (x + 0.044715 * torch.pow(x, 3))
        ))

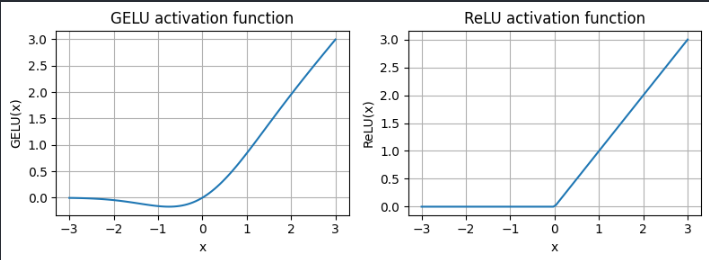
对比 GELU 和 ReLU：

GELU 的平滑特性可以在训练过程中带来更好的优化效果，因为它允许模型参数进行更细微的调整。相比之下，ReLU 在零点处有一个尖锐的拐角，有时会使得优化过程更加困难，特别是在深度或复杂的网络结构中。此外，ReLU 对负输入的输出为0，而 GELU 对负输入会输出一个小的非零值。这意味着在训练过程中，接收到负输入的神经元仍然可以参与学习，只是贡献程度不如正输入大。

接下来定义前馈网络：

class FeedForward(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        self.layers = nn.Sequential(
            nn.Linear(cfg["emb_dim"], 4 * cfg["emb_dim"]),
            GELU(),
            nn.Linear(4 * cfg["emb_dim"], cfg["emb_dim"]),
        )
    #运行一次就线性两次激活一次
    def forward(self, x):
        return self.layers(x)

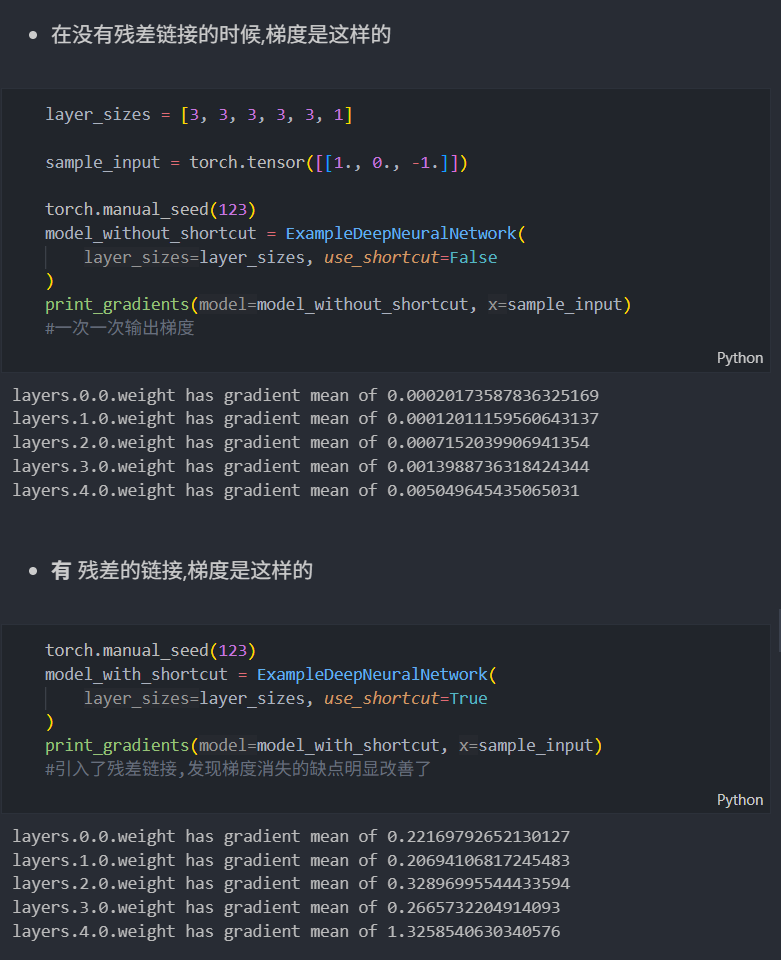
添加快捷连接（残差）

用于计算机视觉中的深度网络（特别是残差网络），目的是缓解梯度消失问题。梯度消失问题指的是在训练过程中，梯度在反向传播时逐渐变小，导致早期网络层难以有效训练。

对比：

连接 Transformer 块中的注意力层和线性层

代码如下：

class TransformerBlock(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        self.att = MultiHeadAttention(
            d_in=cfg["emb_dim"],               # 输入特征维度
            d_out=cfg["emb_dim"],              # 输出特征维度
            context_length=cfg["context_length"],  # 上下文长度
            num_heads=cfg["n_heads"],          # 注意力头的数量
            dropout=cfg["drop_rate"],          # Dropout 比例
            qkv_bias=cfg["qkv_bias"]           # 查询、键和值的偏置
        )  # 多头注意力模块，结合各种参数
        self.ff = FeedForward(cfg)  # 前馈神经网络模块
        self.norm1 = LayerNorm(cfg["emb_dim"])  # 第一归一化层
        self.norm2 = LayerNorm(cfg["emb_dim"])  # 第二归一化层
        self.drop_shortcut = nn.Dropout(cfg["drop_rate"])  # 残差连接的 Dropout

    def forward(self, x):
        # 对注意力模块的快捷连接
        shortcut = x
        x = self.norm1(x)  # 应用第一归一化层
        x = self.att(x)  # 通过多头注意力模块，形状为 [batch_size, num_tokens, emb_size]
        x = self.drop_shortcut(x)  # 应用 Dropout
        x = x + shortcut  # 将原始输入加回，实现残差连接

        # 对前馈网络模块的残差连接
        shortcut = x
        x = self.norm2(x)  # 应用第二归一化层
        x = self.ff(x)  # 通过前馈神经网络模块
        x = self.drop_shortcut(x)  # 应用 Dropout
        x = x + shortcut  # 将原始输入加回，实现残差连接

        return x

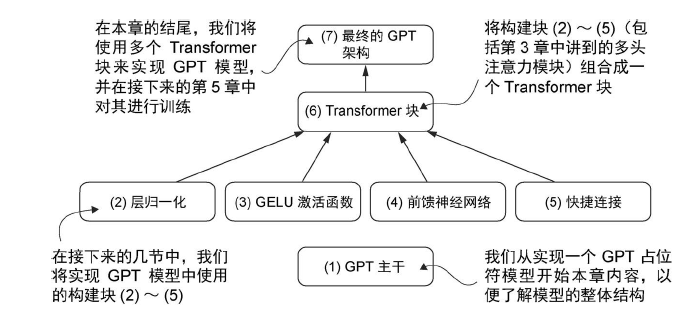
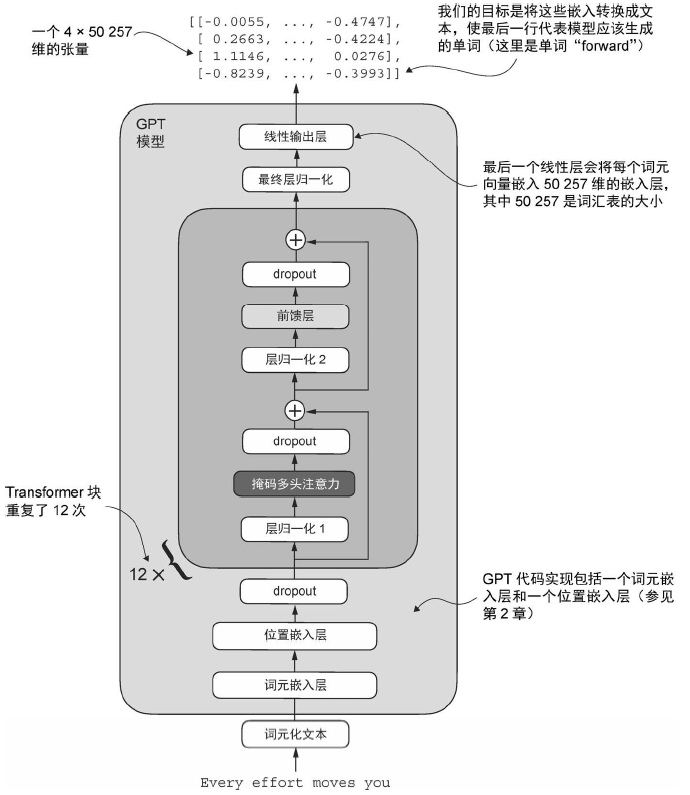
实现 GPT 模型

class GPTModel(nn.Module):#召唤GPT!
    def __init__(self, cfg):
        super().__init__()
        self.tok_emb = nn.Embedding(cfg["vocab_size"], cfg["emb_dim"])
        self.pos_emb = nn.Embedding(cfg["context_length"], cfg["emb_dim"])
        self.drop_emb = nn.Dropout(cfg["drop_rate"])
        #新建字典、位置信息、还有dropout的比率设置
        self.trf_blocks = nn.Sequential(
            *[TransformerBlock(cfg) for _ in range(cfg["n_layers"])])
        #解包操作

        self.trf_blocks = nn.Sequential(
        TransformerBlock(cfg),
        TransformerBlock(cfg),
        TransformerBlock(cfg)
                )
        self.final_norm = LayerNorm(cfg["emb_dim"])
        #归一化
        self.out_head = nn.Linear(
            cfg["emb_dim"], cfg["vocab_size"], bias=False
        )
        #输出头保证维度
    def forward(self, in_idx):
        batch_size, seq_len = in_idx.shape
        tok_embeds = self.tok_emb(in_idx)
        pos_embeds = self.pos_emb(torch.arange(seq_len, device=in_idx.device))
        x = tok_embeds + pos_embeds  # Shape [batch_size, num_tokens, emb_size]
        x = self.drop_emb(x)
        x = self.trf_blocks(x)
        x = self.final_norm(x)
        logits = self.out_head(x)
        return logits

可以通过以下代码计算模型参数：

1
2
3

total_params = sum(p.numel() for p in model.parameters())
#模型的总参数数量
print(f"Total number of parameters: {total_params:,}")

发现输出大概为 1.6 亿。这是因为在原始 GPT-2 论文中，研究人员采用了权重共享（weight tying）技术，即将标记嵌入层（tok_emb）作为输出层复用，具体表现为设置 self.out_head.weight = self.tok_emb.weight。

文本生成

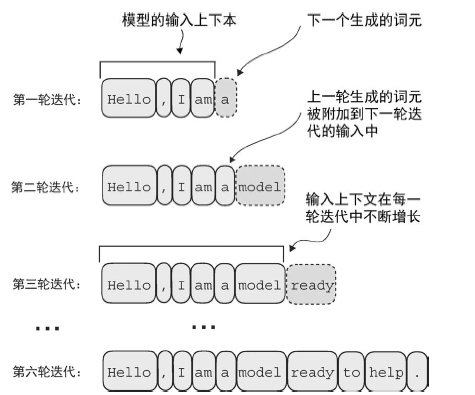
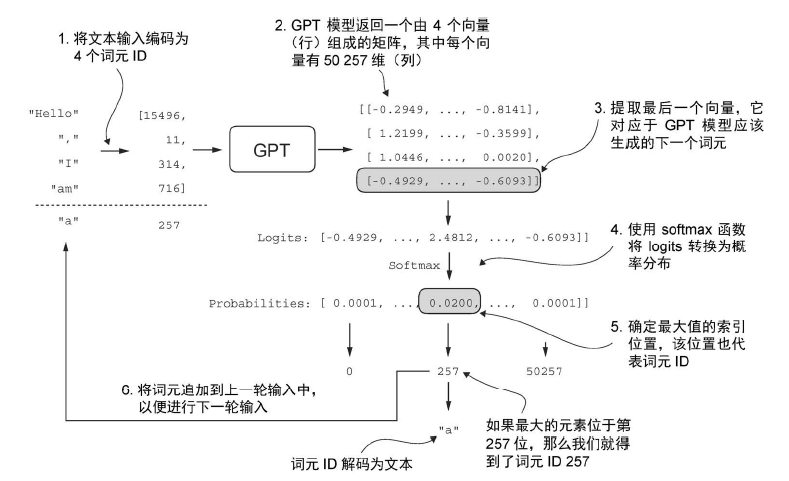
大模型在每次生成文本时，需要把上一次预测的结果添加到上下文中，然后再进行生成。在每一步中，模型输出一个矩阵，其中的向量表示有可能的下一个词元。将与下一个词元对应的向量提取出来，并通过 softmax 函数转换为概率分布。在包含这些概率分数的向量中，找到最高值的索引，这个索引对应于词元ID。然后将这个词元 ID 解码为文本，生成序列中的下一个词元。最后，将这个词元附加到之前的输入中，形成新的输入序列，供下一次迭代使用。这个逐步的过程使得模型能够按顺序生成文本，从最初的输入上下文中构建连贯的短语和句子。

以下的 generate_text_simple 函数实现了贪心解码（greedy decoding），这是一种简单且快速的文本生成方法。
在贪心解码中，模型在每一步选择具有最高概率的词（或标记）作为下一个输出（由于最高的 logit 值对应最高的概率，实际上我们不需要显式地计算 softmax 函数）。

def generate_text_simple(model, idx, max_new_tokens, context_size):
    # 预测单词的模块
    # idx 是当前上下文中的（batch, n_tokens）索引数组
    for _ in range(max_new_tokens):
        # 每次生成一个单词后，重新将其加入序列中
        # 如果当前上下文长度超过模型支持的最大上下文长度，则截取
        # 例如，如果LLM只支持5个token，而上下文长度为10
        # 那么只使用最后5个token作为上下文
        idx_cond = idx[:, -context_size:]
        # 如果idx的长度超过模型支持的上下文长度size，只保留最后size个token
        # 避免溢出
        # 获取预测结果
        with torch.no_grad():  # 在推理阶段，不需要计算梯度，因为没有反向传播
            # 这样可以减少存储开销
            logits = model(idx_cond)
            # 模型输出结果
        # 只关注最后一个时间步的输出
        # (batch, n_tokens, vocab_size) 变为 (batch, vocab_size)
        logits = logits[:, -1, :]
        # 关注最后一个时间步
        # 使用softmax函数计算概率
        probas = torch.softmax(logits, dim=-1)  # (batch, vocab_size)
        # 归一化
        # 获取具有最高概率值的词汇索引
        idx_next = torch.argmax(probas, dim=-1, keepdim=True)  # (batch, 1)
        # 获取概率最高的词汇索引
        # 将采样的索引添加到序列中
        idx = torch.cat((idx, idx_next), dim=1)  # (batch, n_tokens+1)

    return idx